We have new published research that has implications for why global mean surface air temperature (GMT) is stable in the absence of external radiative forcings.

One of the central differences between weather prediction and climate projection is that the former is considered to be an “initial value problem” and the latter is considered to be a “forced boundary condition problem” (1). This dichotomy implies that weather is subject to chaotic variability and thus is fundamentally unpredictable beyond several weeks but climate can be projected into the future with some confidence as long as changes in the boundary conditions of the system are known (2). For GMT, the fundamental boundary conditions are the system’s basic radiative properties, i.e., the incoming solar radiation, planetary albedo, and the atmospheric infrared transitivity governed by greenhouse gas concentrations (3).

In reality, however, the forced boundary condition paradigm is complicated by nonlinear, two-way, interactions within the climate system. In particular, planetary albedo and the greenhouse effect are themselves complex functions of GMT and its spatial distribution (4). Therefore, if GMT is to be projected to within some fairly narrow range for a given change in boundary conditions (i.e., an increase in the greenhouse effect), it must be the case that the climate system can damp any unforced (internally generated) GMT perturbations. This idea becomes clearer when GMT evolution is expressed as a perturbation away from an equilibrium value set by the boundary conditions (ΔT=GMT-GMT_equilibrium). ΔT change can be expressed as the sum of forcings (F), feedbacks (λΔT) and heat fluxes between the upper ocean’s mixed layer and the ocean below the mixed layer (Q),

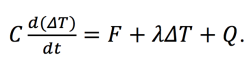.                                                                                            [1]

In this formulation, F often represents external radiative forcings (e.g., changes in well-mixed greenhouse gasses, aerosol loading, incoming solar radiation, etc.), however, here we are concerned with the stability of ΔT in the absence of external forcings so F represents unforced energy imbalances at the top of the atmosphere (TOA) (5). C is the effective heat capacity of the land/atmosphere/ocean-mixed-layer system, λ is the feedback parameter (the reciprocal of the climate sensitivity parameter) and λΔT represents the radiative fast-feedbacks (positive downward) (6-11).

It is accepted that ΔT should be stable in the long run mostly because of the direct blackbody response of outgoing longwave radiation to ΔT change, which is often referred to as the Planck Response,

                                                                                [2]

where T_e is the effective radiating temperature of the Earth (≈255K) and σ is the Stefan-Boltzmann constant (12). The negative sign indicates increased energy loss by the climate system with warming. λ_Planck is typically incorporated into λ in [1] as the reference sensitivity, e.g., λ=(1−f_a)λ_Planck, where f_a denotes the feedback factor sum of the fast-feedbacks in the system (i.e., water vapor, lapse rate, surface albedo, and cloud feedbacks) (7). Net positive fast-feedbacks imply f_a > 0. Therefore, larger positive fast feedbacks imply a less negative λ and a climate system that is less effective at damping ΔT anomalies. To make this idea more explicit, [1] can be discretized and rearranged to obtain,

                                                                                          [3]

where,                                                                                                                                                                                                                                                                                                  [4]

and

                                                                                               [5]

Now ΔT evolution is explicitly represented as a first-order autoregressive function. In this form, θ is the autoregressive parameter that can be thought of as a quantitative representation of the restoring force, or stability of ΔT. Thus it becomes evident that the relative magnitude of the fast-feedbacks in the system will play a central role in our ability to consider GMT as a forced boundary condition problem. In particular, when θ is positive, but << 1, the system experiences a strong restoring force and ΔT is heavily damped. However, when the feedbacks in the climate system nearly overwhelm the Planck Response (f_a à 1, θ à 1), the restoring force for ΔT disappears. With no restoring force, ΔT would be free to evolve in a chaotic and unpredictable manner comparable to Brownian motion or a “random walk” (13). In this case, GMT could be considered to be “intransitive” (14) and it might be better categorized as an initial value problem than as a forced boundary condition problem.

Consequently, most of modern climate science rests critically on the notion that the Planck Response overwhelms positive radiative fast-feedbacks in the climate system. In our paper, however, we document that at the local level, positive fast-feedbacks actually overwhelm the Planck Response over most of the surface of the Earth. The objective of the paper was to investigate how this finding can be reconciled with an apparently stable GMT at the global spatial scale.

We resolved this apparent paradox by showing that an anomalously warm Earth tends to restore equilibrium in complex and previously unappreciated ways. Our study shows in detail why global temperature should be stable in the absence of external forcings and therefore why global temperature does not evolve chaotically in the long run. Therefore this work explains why large, sustained, changes in global temperature require external radiative forcings like increases in greenhouse gas concentrations.

We focused our analysis on 27 Atmosphere-Ocean General Circulation Models (AOGCMs) from the Coupled Model Intercomparison Project – Phase 5 (CMIP5) (15). We utilize unforced preindustrial control runs which, by definition, included no external radiative forcings and thus all variability emerged spontaneously from the internal dynamics of the modeled climate system. We used the first 200 years of each AOGCMs preindustrial control run and we linearly detrended all analyzed variables so that our analysis was not contaminated with possibly unphysical model drift that may have been a result of insufficient model spin-up. Because this detrending procedure forced the AOGCM runs to be stable over the 200-year period, we are implicitly studying the restoring force for ΔT relative to any 200-year trend present in the control runs. Consequently, we are limited to studying the physical explanation for the stability of ΔT at timescales smaller than 200-years.

For more information see the AGU poster or the paper:

Brown, P.T., W. Li, J.H. Jiang, H. Su (2016) Unforced surface air temperature variability and its contrasting relationship with the anomalous TOA energy flux at local and global spatial scales. Journal of Climate, doi:10.1175/JCLI-D-15-0384.1

References:

1. Kirtman et al. (2013) Near-term Climate Change: Projections and Predictability. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA).
2. Hawkins E & Sutton R (2009) The Potential to Narrow Uncertainty in Regional Climate Predictions. Bulletin of the American Meteorological Society 90(8):1095-1107.
3. Sagan C & Mullen G (1972) Earth and Mars: Evolution of Atmospheres and Surface Temperatures. Science 177(4043):52-56.
4. Armour KC, Bitz CM, & Roe GH (2012) Time-Varying Climate Sensitivity from Regional Feedbacks. Journal of Climate 26(13):4518-4534.
5. Brown PT, Li W, Li L, & Ming Y (2014) Top-of-Atmosphere Radiative Contribution to Unforced Decadal Global Temperature Variability in Climate Models. Geophysical Research Letters:2014GL060625.
6. Wigley TML & Schlesinger ME (1985) Analytical solution for the effect of increasing CO2 on global mean temperature. Nature 315(6021):649-652.
7. Baker MB & Roe GH (2009) The Shape of Things to Come: Why Is Climate Change So Predictable? Journal of Climate 22(17):4574-4589.
8. Geoffroy O, et al. (2012) Transient Climate Response in a Two-Layer Energy-Balance Model. Part I: Analytical Solution and Parameter Calibration Using CMIP5 AOGCM Experiments. Journal of Climate 26(6):1841-1857.
9. Held IM, et al. (2010) Probing the Fast and Slow Components of Global Warming by Returning Abruptly to Preindustrial Forcing. Journal of Climate 23(9):2418-2427.
10. Wigley TML & Raper SCB (1990) Natural variability of the climate system and detection of the greenhouse effect. Nature 344(6264):324-327.
11. Dickinson RE (1981) Convergence Rate and Stability of Ocean-Atmosphere Coupling Schemes with a Zero-Dimensional Climate Model. Journal of the Atmospheric Sciences 38(10):2112-2120.
12. Hansen J. AL, D. Rind, G. Russell,P. Stone , et al. (1984) Climate Sensitivity: analysis of feedback mechanisms. . in Climate Processes and Climate Sensitivity, ed. JE Hansen, T Takahashi, Geophys. Monogr (Washington, DC: Am. Geophys. Union), pp 130-163.
13. Hasselmann K (1976) Stochastic climate models Part I. Theory. Tellus 28(6):473-485.
14. Lorenz E (1968) Climatic Determinism. Meteor. Monographs, Amer. Meteor. Soc. 25:1-3.
15. Taylor KE, Stouffer RJ, & Meehl GA (2011) An Overview of CMIP5 and the Experiment Design. Bulletin of the American Meteorological Society 93(4):485-498.